統計數學
統計數學
平均數 (mean)
為集中趨勢的最常用測度值,目的是確定一組數據的均衡點。
樣本平均數(或簡稱平均數)是一組樣本 $x_{1}, x_{2}, x_{3}…, x_{n}$ 的和,除以樣本的數量。其通常記作 $\overline{x}$(唸 x bar)),其計算式如下:
$$
\overline{x}=\frac{x_{1}+x_{2}+\cdots+x_{n}}{n}
$$
其公式如下:
$$
\overline{x}=\frac{1}{n}\left(x_{1}+x_{2}+\cdots+x_{n}\right)=\frac{1}{n} \sum_{i=1}^{n} x_{i}
$$
$xi=$ 數據個別值
$i=i~n$
$n=$ 樣本數大小
而在統計學中,母體所有數的平均數稱之為「母體平均數」以 $μ$ (唸mu) 表示。
眾數 (mode)
眾數是指一組數據中出現次數最多的那個數據,一組數據可以有多個眾數,也可以沒有眾數。
中位數(median)
中位數是指將數據按大小順序排列起來,形成一個數列,居於數列中間位置的那個數據。中位數用Me表示。
從中位數的定義可知,所研究的數據中有一半小於中位數,一半大於中位數。中位數的作用與算術平均數相近,也是作為所研究數據的代表值。在一個等差數列或一個正態分佈數列中,中位數就等於算術平均數。
在數列中出現了極端變數值的情況下,用中位數作為代表值要比用算術平均數更好,因為中位數不受極端變數值的影響;如果研究目的就是為了反映中間水平,當然也應該用中位數。在統計數據的處理和分析時,可結合使用中位數。
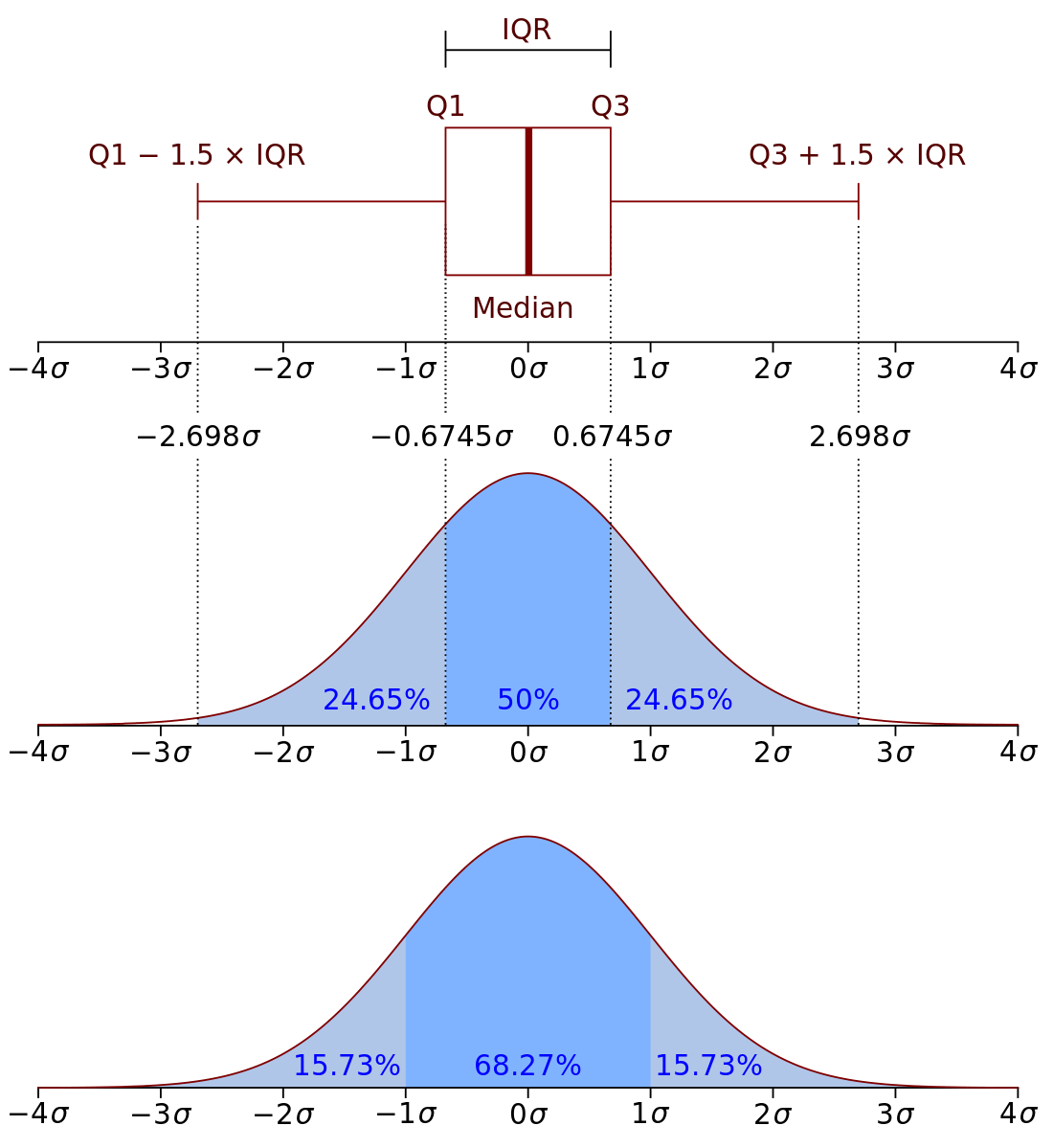
四分位數 (Quartile)
四分位數是統計學中分位數的一種,即把所有數值由小到大置換並分成四等份,處於三個分割點位置的數值就是四分位數。
- 第一四分位數($Q_{1}$),又稱較小四分位數,等於該樣本中所有數值由小到大置換後第25%的數字。
- 第二四分位數($Q_{2}$),又稱中位數,等於該樣本中所有數值由小到大置換後第50%的數字。
- 第三四分位數($Q_{3}$),又稱較大四分位數,等於該樣本中所有數值由小到大置換後第75%的數字。
第三四分位數與第一四分位數的差距又稱四分位距(InterQuartile Range, IQR)。
四分位距(interquartile range, IQR)
是描述統計學中的一種方法,以確定第三四分位數和第一四分位數的分別 (即 $Q_{1}$, $Q_{3}$ 的差距)。與變異數、標準差一樣,表示統計資料中各變量分散情形,但四分差更多為一種穩健統計(robust statistic)。
其公式如下:
$$
\mathrm{IQR}=Q_{3}-Q_{1}
$$
四分位差 (Quartile Deviation, QD)
是 $Q_{1}$、$Q_{2}$ 的差距的一半,其公式如下:
$$
\mathrm{QD}=\frac{Q_{3}-Q_{1}}{2}
$$
變異數 (Variance)
變異數又稱方差,變異數即在量測所有資料到平均數的平均距離。一個很自然會被想到用來量測資料分散程度之指標值為平均絕對離差。但絕對值在代數運算上較麻煩,因此將絕對值以平方來替代變異數會因資料中少數幾筆特別大或特別小的值,使變異數變得特別大。
設有一組母體資料 $x_{1}, x_{2}, x_{3}…, x_{n}$:且 $u$ 為此組母體資料之平均數,則母體變異數 $σ^2$ 為
$$
\sigma^{2}=\frac{\sum_{i=1}^{N}\left(X_{i}-\mu\right)^{2}}{N}
$$
設有一組樣本資料 $x_{1}, x_{2}, x_{3}…, x_{n}$:且 $\overline{x}$ 為此組樣本資料之平均數,則母體變異數 $s^2$ 為
$$
s^{2}=\frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}{n-1}
$$
範例一
小成第一次的段考成績為國文96分、數學90分、英文85分、地理78分、 歷史92分、理化67分,請問小成成績的變異數為多少?
根據平均數的定義,將成績總和除以科目個數:
(96+90+85+78+92+67)/6 = 508/6 = 84.67
小成第一次段考的平均分數為 84.67 分
所以其成積的變異數為:
$$
\begin{array}{l}{\frac{(96-84.67)^{2}+(90-84.67)^{2}+\ldots+(67-84.67)^{2}}{6}} \ {=94.56(分)^{2}}\end{array}
$$
範例二
測試五個燈泡的使用壽命長度(單位:小時),資料分別為 867、849、840、852、822 試求燈泡壽命的變異數。
算術平均數等於五個燈泡的壽命總和除以燈泡個數:
(867+849+840+852+822)/5 = 4230/5 = 846
所以燈泡的平均壽命為 846 小時
$$
\begin{array}{l}{\frac{(867-846)^{2}+(849-846)^{2}+\ldots+(822-846)^{2}}{5}} \
{=846(小時)^{2}}\end{array}
$$
變異係數 (Coefficient of Variation, CV)
變異係數(CV)是標準差除以平均數所得的百分比值(單位:%),數值不會受到量測單位影響
設此組資料的平均數為 $\overline{x}$,標準差為 s,則其變異係數為
$$
C V=\frac{s}{\overline{x}}
$$
範例
調查五位學生之身高及體重如下,試比較其分散程度。身高:172、168、164、170、176 (公分);體重:62、57、58、64、64 (公斤)
因為身高與體重的單位不同,欲比較二者的分散程度,可利用變異係數來比較。先計算身高與體重各自的平均數與標準差,得平均身高為 170 公分、標準差為 4.47 公斤,平均體重為 61 公斤、標準差為3.31公斤。
計算身高的變異係數為
4.47/170×100% = 2.63 %
而體重的變異係數為
3.31/61×100% = 5.4%
比較二者,體重的變異係數較大,所以體重的分散程度較大。
標準差 (Standard Deviation, SD)
數學符號 $σ$ ,為變異數開平方根,反映組內個體間的離散程度;標準差與期望值之比為標準離差率。
設有一組母體資料 $x_{1}, x_{2}, x_{3}…, x_{n}$,$u$ 為此組資料之平均數,則母體標準差即母體異數的開平方
$$
\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^{N}\left(X_{i}-\mu\right)^{2}}
$$
設有一組樣本資料 $x_{1}, x_{2}, x_{3}…, x_{n}$,$\overline{x}$ 為此組資料之平均數,則樣本標準差即樣本變異數的開平方
$$
s=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\overline{x}\right)^{2}}
$$
範例一
小成第一次的段考成績為國文 96 分、數學 90 分、英文 85 分、地理 78 分、 歷史 92 分、理化 67 分,請問小成成績的標準差為多少?
根據平均數的定義,將成績總和除以科目個數:
(96+90+85+78+92+67)/6 = 508/6 = 84.67
小成第一次段考的平均分數為84.67分
所以其成積的標準差為:
$$
\begin{array}{l}{\sqrt{\frac{(96-84.67)^{2}+\ldots+(67-84.67)^{2}}{6}}} \ {=9.72(分)}\end{array}
$$
範例二
測試五個燈泡的使用壽命長度(單位:小時),資料分別為 867、849、840、852、822 試求燈泡的平均壽命。
算術平均數等於五個燈泡的壽命總和除以燈泡個數
(867+849+840+852+822)/5 = 4230/5 = 846
所以燈泡的平均壽命為 846 小時
而此五個燈泡壽命的標準差為:
$$
\begin{array}{l}{\sqrt{\frac{(867-846)^{2}+\ldots+(822-846)^{2}}{5}}} \ {=14.82(小時)}\end{array}
$$
均方誤差 (Mean Squared Error, MSE)
均方誤差是指參數估計值與參數真值之差平方的期望值;
MSE可以評價數據的變化程度,MSE的值越小,說明預測模型描述實驗數據具有更好的精確度。
$$
M S E=\frac{1}{n} \sum_{i=1}^{n}\left(實際值-\text 估計值\right)^{2}
$$
均方根誤差 (Root-Mean-Square Error, RMSE)
均方根誤差是均方誤差的算術平方根
觀測值
$$
R M S E=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(實際值-估計值\right)^{2}}
$$
##平均絕對誤差 (Mean Absolute Error, MAE)
平均絕對誤差是絕對誤差的平均值,平均絕對誤差能更好地反映預測值誤差的實際情況.
$$
M A E=\frac{1}{n} \sum_{i=1}^{n}\left|\left(f_{i}-y_{i}\right)\right|
$$
$f_{i}為第 i 項的實際值$
$y_{i}為第 i 項的估計值$