關於 Transform Matrix
關於 Transform Matrix
最近在解一些關於影像的平移與縮放變換,順手紀錄一下相關數學原理。
在 Transform 中,它有四個相關屬性,分別是 Translate (位移)、Scale (縮放)、Rotate (旋轉)、Skew (傾斜)。
Transform 是以 Matrix 作為展開。
一個基本的 Transform Matrix 如下
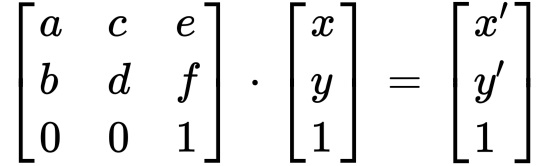
其轉換公式如下
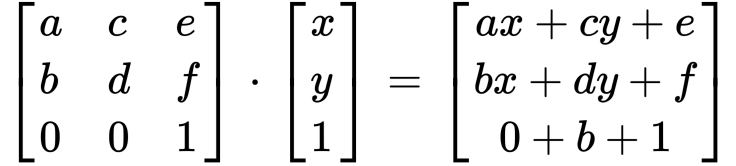
其中
x' = ax + cy + e 為變換後的水平座標
y' = bx + dy + f 為變換後的垂直座標
Matrix 表示法:Transform: Matrix (a, b, c, d, e, f)
各種轉換其實都可以將型式變成「圖片上的點用齊次座標表示後乘上一個轉換矩陣 M」
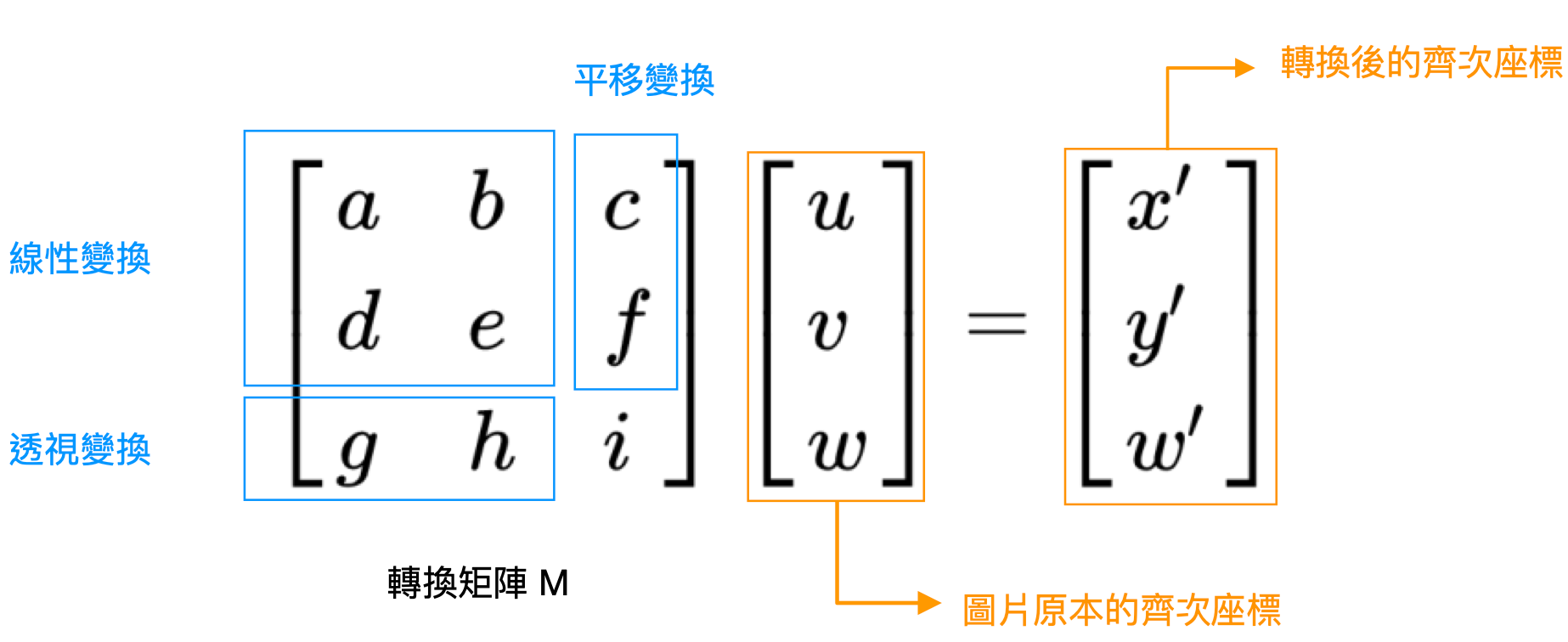
Translate (位移)
其關鍵參數為 e, f
e = 欲移動之水平距離f = 欲移動之垂直距離
當原始點 (x, y)=0,移至新點 (x’, y’) = (20, 20),其表達式如下
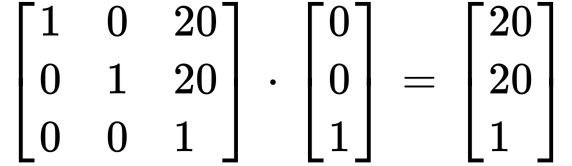
Matrix 表示法:**Transform: Matrix (1, 0, 0, 1, 20, 20),同等於 Transform: Tranlate (20px, 20px)
scale (縮放)
其關鍵參數為 a, d
a = 欲縮放之 x 軸d = 欲縮放之 y 軸
欲將影像放大兩倍,其表達式如下
x’ 座標會是原來 x 座標的兩倍;y’ 座標是原來 y 座標的兩倍
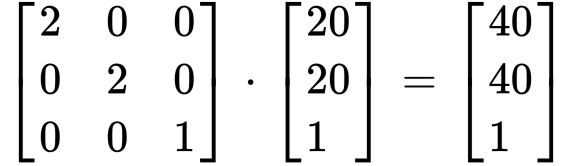
Matrix 表示法:**Transform: Matrix (2, 0, 0, 2, 0, 0),同等於 Transform: Scale (2, 2)
Rotate (旋轉)
Rotae 涉及角度的轉換,需要以三角函數計算角度的變換,轉換公式如下
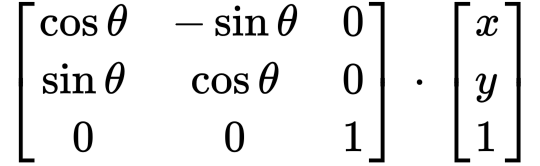
其中
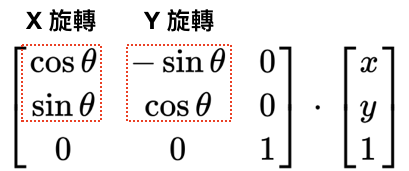
計算式如下
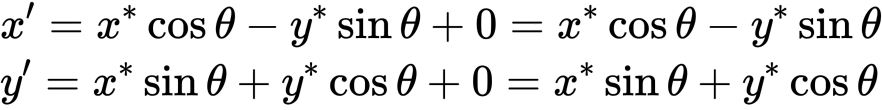
欲將影像旋轉 60°,其表達式如下
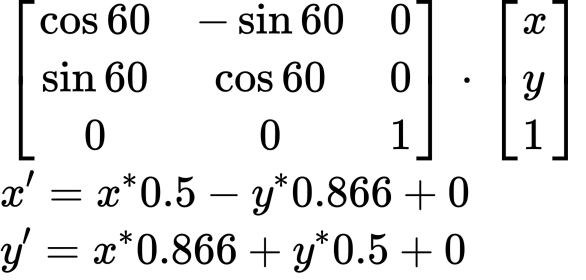
Matrix 表示法:**Transform: Matrix (0.5, 0.866, -0.866, 0.5, 0, 0),同等於 Transform: Rotate (60deg)
Skew (傾斜)
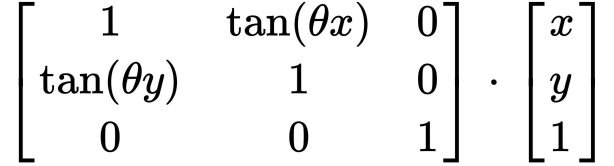
其中,θx 表示 x 軸傾斜的角度,θy 表示 y 軸,兩者並無關聯。
其他
如果目標圖形以(x , y )為軸心順時針旋轉 θ 弧度,其變換矩陣如下
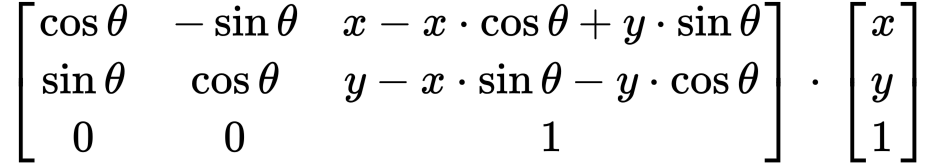
Be the first person to leave a comment!